Teorema fundamental de la geometría de Riemann
Mira otros diccionarios:
Teorema fundamental de la geometría de Riemann — En geometría de Riemann, el teorema fundamental de la geometría de Riemann establece que dado una variedad de Riemann (o una variedad seudoriemanniana) hay una única conexión libre de torsión que preserva el tensor métrico. Tal conexión se llama… … Wikipedia Español
Geometría de Riemann — En geometría diferencial, la geometría de Riemann es el estudio de las variedades diferenciales con métricas de Riemann; es decir de una aplicación que a cada punto de la variedad, le asigna una forma cuadrática definida positiva en su espacio… … Wikipedia Español
Geometría riemanniana — Saltar a navegación, búsqueda En geometría diferencial, la geometría riemanniana es el estudio de las variedades diferenciales con métricas de Riemann; es decir de una aplicación que a cada punto de la variedad, le asigna una forma cuadrática… … Wikipedia Español
Geometría diferencial de curvas — En matemáticas, la geometría diferencial de curvas propone definiciones y métodos para analizar curvas simples en Variedades de Riemann, y en particular, en el Espacio Euclídeo. Contenido 1 Longitud de arco 2 Vectores tangente, normal y binormal … Wikipedia Español
Historia de la geometría — La geometría es una de las más antiguas ciencias. Inicialmente, constituía un cuerpo de conocimientos prácticos en relación con las longitudes, áreas y volúmenes. En el Antiguo Egipto estaba muy desarrollada, según los textos de Heródoto,… … Wikipedia Español
Semejanza (geometría) — Dos triángulos son semejantes si existe una relación de semejanza o similitud entre ambos. Contenido 1 Introducción 2 Ecuación 2.1 Corolarios … Wikipedia Español
Variedad pseudoriemanniana — Matemáticamente el espacio tiempo curvo que usa la teoría de la relatividad es un variedad pseudoriemanniana con curvatura dada por la densidad de energía impulso. En geometría diferencial, una variedad pseudoriemanniana es una variedad… … Wikipedia Español
Conexión de Levi-Civita — En geometría de Riemann, la conexión de Levi Civita (nombrada así por Tullio Levi Civita) es la conexión libre de torsión del fibrado tangente, preservando una métrica de Riemann (o métrica pseudoriemanniana) dada. El teorema fundamental de la… … Wikipedia Español
Conexión de Levi-Civita — En geometría de Riemann, la conexión de Levi Civita (nombrada así por Tullio Levi Civita) es la conexión libre de torsión del fibrado tangente, preservando una métrica de Riemann (o métrica seudoriemanniana) dada. El teorema fundamental de la… … Enciclopedia Universal
Anexo:Matemáticos importantes — En esta lista de matemáticos importantes se presenta una selección de matemáticos desde la antigüedad hasta el presente. La selección se orienta por los aportes científicos, utilizando como criterio para definir el grado de notoriedad la atención … Wikipedia Español
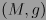 una variedad de Riemann (o variedad seudoriemanniana) entonces hay una conexión única
una variedad de Riemann (o variedad seudoriemanniana) entonces hay una conexión única 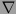 que satisface las condiciones siguientes:
1. para cualesquiera campos vectoriales
que satisface las condiciones siguientes:
1. para cualesquiera campos vectoriales 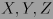 tenemos
tenemos 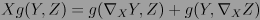 , donde
, donde 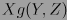 denota la derivada de la función
denota la derivada de la función 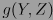 a lo largo del campo vectorial
a lo largo del campo vectorial 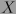 .
2. para cualesquiera campos vectoriales
.
2. para cualesquiera campos vectoriales 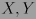 tenemos
tenemos 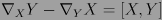 , donde
, donde 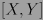 denota el corchete de Lie para los campos vectoriales
denota el corchete de Lie para los campos vectoriales 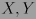 .
.